Abstract
Curvilinearly stiffened plates can have superior mechanical properties than traditional straight-line stiffened plates. To avoid the shear locking problem in the modeling of stiffened thick plates by Reissner-Mindlin theory when the thickness of plate decrease, discrete shear triangle element was introduced by employing the discrete shear constraints on each side. The discrete shear triangle element is employed for the plate and the Timoshenko beam theory is employed for the curvilinearly stiffeners, respectively. The FE equations are established through displacement interpolation function of plate and the displacement compatibility conditions at the plate-stiffened interfaces. The plate and stiffener are modeled separately in the present method, which allows the nodes of stiffener element not coincide with nodes of the plate’s shell-element. Based on the newly proposed modeling technique, the statics, vibration and buckling behavior of curvilinearly stiffened plates are investigated. Numerical and experimental investigations are conducted to verify the mechanical properties of proposed model for stiffened plates. Results from the proposed method show good agreements with the numerical and experimental results. The present method can conduct static and dynamic analysis for both stiffened thick and thin plates and guarantee the accuracy of calculation with less number of elements.
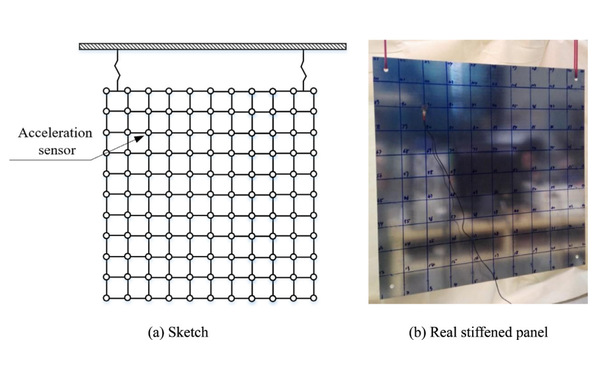
Fig. Node information on the plate and the placement of the acceleration sensor
原文链接:http://doi.org/10.1016/j.ijmecsci.2019.105286


